18.785: Analytic Number Theory (MIT, Spring 2007)

Added 28 Oct 2015: an updated version of these notes will be kept here.

This is the web page for the course 18.785 (Analytic Number Theory), which was taught at MIT in the spring 2007 semester. This course was an introduction to analytic number theory, including the use of zeta functions and L-functions to prove distribution results concerning prime numbers (e.g., the prime number theorem in arithmetic progressions). The principal goal was to present the following theorem of Goldston, Pintz, and Yildirim (2005): if p_n denotes the n-th prime number, then

There is also a bit of discussion of non-abelian equidistribution results, like the Chebotarev density theorem, and the Sato-Tate conjecture for elliptic curves (and recent progress on same by Clozel, Harris, Shepherd-Barron, Taylor).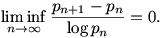

Instructor

The course instructor was Kiran Kedlaya. The course grader was Ruochuan Liu (ruochuan at math dot mit dot edu).

On this site

• Course syllabus
• Lecture calendar (includes notes)

Problem sets

The lecture notes I distribute in class and online will come with exercises attached; the problem sets will be extracted from these, as detailed below.

Problem sets are due in class on the indicated dates. However, I tend to be pretty flexible about extensions in graduate courses, provided you ask in advance. (You are free to ask not in advance, but at your own risk.)

• PS 1 (due 2/14): exercises 1-8 from The prime number theorem.
• PS 2 (due 2/21): exercises 1-10 from Dirichlet series and arithmetic functions.
• PS 3 (due 2/28): exercises 1-5 from Dirichlet characters and Dirichlet L-functions, and exercises 1-6 from Primes in arithmetic progressions.
• PS 4 (due 3/7): exercises 1-5 from The functional equation for the Riemann zeta function, exercises 1-4 from The functional equations for Dirichlet L-functions.
• PS 5 (due 3/21): exercises 5-9 from The functional equations for Dirichlet L-functions, exercise 1 from Error bounds in the prime number theorem, exercises 1-6 from More on the zeroes of zeta.
• PS 6 (due 4/4): exercises 1-4 from von Mangoldt's formula; exercises 1-6 from Revisiting the sieve of Eratosthenes.
• PS 7 (due 4/11): exercises 1-2 from Brun's combinatorial sieve, exercises 1-5 from The Selberg sieve.
• PS 8 (due 4/18): exercises 6-9 from The Selberg sieve; exercises 1-5 from Applying the Selberg sieve.
• PS 9 (due 4/25): exercises 1-4 from Introduction to large sieve inequalities; exercises 1-3 from A multiplicative large sieve inequality.
• PS 10 (due 5/2): exercises 1-2 from The Bombieri-Vinogradov theorem (statement); exercises 1-5 from The Bombieri-Vinogradov theorem (proof).
• PS 11 (due 5/9): exercises 1-5 from Prime k-tuples; exercises 1-3 from Short gaps between primes (after Goldston-Pintz-Yildirim).